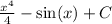Question

Integral (x pangkat 3 - cos x) dx

Answer 1

You can break the integral of a sum/difference into the sum/difference of the integrals:

`\int (x^3-\cos(x))\;dx = \int x^3\; dx - \int \cos(x)\; dx`

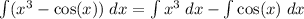
The first integral can be solved using the power rule for integrations:

`\int x^n\; dx = (x^(n+1))/(n+1) \implies \int x^3\; dx = (x^4)/(4)`

As for the second, remember the chain of derivation of trigonometric functions:

`\sin(x) \to \cos(x) \to -\sin(x) \to -\cos(x) \to \sin(x) \ldots`

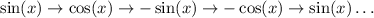
The integration chain is the same, but it follows the opposite direction: the integral of the cosine function is the sine function. So, you have

`- \int \cos(x)\; dx = -\sin(x)`

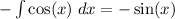
Since this is an indefinite integral, we must add the generic costant to the answer:

`(x^4)/(4) -\sin(x) + C`