Question

A company produces precision 1 meter (1000 mm) rulers. the actual distribution of lengths of the rulers produced by this company is normal, with mean μ and standard deviation σ = 0.02 mm. suppose i select a simple random sample of four of the rulers produced by the company and i measure their lengths in mm. the sample yields = 1000. a 90% confidence interval for μ is:

Answer 1

Let X be the length of rulers. X follows Normal distribution with mean μ and standard deviation σ = 0.02. A sample of size n=4 is drawn from population and sample mean m=1000. We have to find 90% confidence interval for population mean μ.

Here population standard deviation is given to us so we will use z confidence interval for mean. It is given as

(Sample mean - Margin of error , Sample mean + Margin of error)

Where margin of error for z confidence interval is

ME = σ
`(z_(\alpha/2))/(√(n))`

Where σ = population standard deviation = 0.02

n= sample size =4

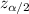`z_(\alpha/2)` = Critical z score value for given confidence level

We have to find here 90% confidence interval so confidence level c= 0.9

α = 1 -c =1-0.9 = 0.1

`z_(\alpha/2)` =
`z_(0.1/2)` =
`z_(0.05)`

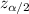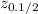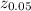
Here we have to find z score value such that area below it is -z is 0.05 and above z is 0.05

Using excel function to find z score value

=NORM.S.INV(0.05) = -1.645

For calculating confidence interval we consider positive z score value which is 1.645

So the margin of error is

ME =
`(0.02 * 1.645)/(√(4))`

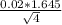
ME = 0.01645

90% confidence interval for mean is

(Sample mean - ME, Sample mean+ME)

1000- 0.01645, 1000+0.01645

(1000.01645, 999.9836)

Rounding interval upto 3 decimal places

(1000.016, 999.984)

90% confidence interval for population mean is (1000.016, 999.984)