2 Answers

Dequin · Answer 1 · 2019-12-12T07:05:15+0000

The other x intercept would be 2.29.

You can find this by first modeling the equation using vertex form: y = a(x - h)^2 + k, in which the variables stand for the following:

a = constant

h = x value of vertex

k = y value of vertex.

Since we know enough to plug in and solve for a, we can get the equation we are using.

y = a(x - h)^2 + k

First put in the vertex points into (h, k)

y = a(x - 1)^2 + 5

Now add the points we know for x and y from the y-intercept

2 = a(0 - 1)^2 + 5

And solve that for a

2 = a(0 - 1)^2 + 5

2 = a (-1)^2 + 5

2 = a + 5

-3 = a

Now we can model the equation as y = -3(x - 1)^2 + 5. Using that, we can distribute to put in standard form.

y = -3(x - 1)^2 + 5

y = -3(x^2 - 2x + 1) + 5

y = -3x^2 + 6x - 3 + 5

y = -3x^2 + 6x + 2

Now we can use the quadratic equation to solve for the remaining zero. Using the following variables:

a = -3 (attached to x^2)

b = 6 (attached to x)

c = 2 (constant)

$\frac{-b +/- \sqrt{b^(2) - 4ac}}{2a}$

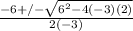
$\frac{-6 +/- \sqrt{6^(2) - 4(-3)(2)}}{2(-3)}$

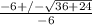
(-6 +/- √(36 + 24))/(-6)

(-6 +/- √(60))/(-6)

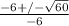
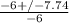
(-6 +/- 7.74)/(-6)

x = 0.29 or x = -2.29

Please log in or register to add a comment.