Question

Maria and Josie are also figuring out the dimensions of the runners’ corral at the start line. To accommodate the number of projected runners, they’ve determined that they need a minimum area of 29,040 square feet in the corral. They have 1,364 feet of temporary fence barriers to set up the corral. They are leaving one end of the rectangular corral open as shown in the image. When the race is about to start, Maria and Josie will remove the fencing barriers on the start line. Create an inequality that represents the relationship between the area of the space and the length of fencing needed.

Answer 1

Let the rectangular coral is x feet wide and y feet long.

Then area is given by (length * width) = xy

Given that minimum area should be 29040 square feet so that means

xy>=29040 ...(i)

Now it says that "They are leaving one end of the rectangular corral open". Which means we have only three sides available for the fence.

Let fence is open along length.

then perimeter of the rectangular corral will be = x+x+y = 2x+y

Given that "They have 1,364 feet of temporary fence barriers to set up the corral"

so that means 2x+y=1364

or

y=1364-2x ...(ii)

Plug (ii) into (i), we get:

`x(1364-2x) \geq 29040`

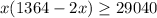
Hence required inequality is
`x(1364-2x) \geq 29040`.

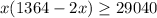You may expand that if needed.