Question

A film student wants to capture a shot of a satellite dish placed at the top of a building. The line of sight between the ground camera and the top of the building is 45 feet, and the angle of the camera with respect to the ground is 50 degrees. What is the height of the building? If necessary, round your answer to the nearest tenth of a foot.

Show the steps used to solve this problem.

Answer 1

The situation in the question can be represented by a right triangle with a hypotenuse of 45 feet and one of the angles as 50 degrees. We are to find the side opposite angle 50 degrees, hence we make use of sine of angles.

Let the height of the building be x, then

`sin(50^o)=\cfrac{opp}{hyp}=\cfrac{x}{45}\\ \\ \Rightarrow x=45sin(50^o)=34.47`

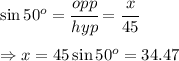
Therefore, the height of the building is 34.5 feet to the nearest tenth of a foot.