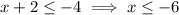Question

Which of the following is the solution

Answer 1

The answer is the second option.

First of all, let's rearrange the inequality by dividing both sides by 4. Since we are dividing by a positive number, we preserve the inequality sign. So, we have

`|x+2| \geq 4`

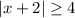
Now, let's focus on what absolute value does in general. The absolute value function
`f(x)=|x|` takes a number as input, and returns the positive version of that input. In other words, if fed with a positive input
`x`, the function will return
`x` itself, since it was already positive. On the contrary, a negative output
`x` yields the output
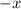`-x`, to make sure that the output is positive.

So, if you want the absolute value of a number to be greater than or equal to 4, you can either take a positive number greater than or equal to 4, or a negative number smaller than or equal to -4. Let me show a couple of example.

If you choose 17, then you have
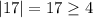`|17|=17\geq4`, which proves that a positive number greater than 4 is a good choice.

Similarly, if you choose -6, then you have
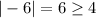`|-6|=6\geq4`, which proves that a negative number smaller than -4 is also a good choice.

Now let's return to our equation: we want

`|x+2| \geq 4`

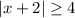
and we just proved that we need the quantity inside the absolute value to be larger than or equal to 4 of less than or equal to -4. In formula, this becomes

`x+2 \geq 4 \implies x \geq 2`

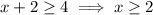
or

`x+2 \leq -4 \implies x \leq -6`