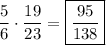Question

By accident, four burned-out bulbs have been mixed in with 20 good ones. Ken is replacing old bulbs in his house. If he selects two bulbs at random from the box of 24, what is the probability they both work?

Answer 1

We will be using the fact that
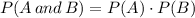`P(A \, and \,B) = P(A) \cdot P(B)`, where
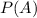`P(A)` is the probability that the first bulb works and
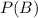`P(B)` is the probability that the second bulb works.

The probability that the first bulb works is
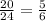`(20)/(24) = (5)/(6)`. However, when we take one out (given that the first bulb works) we now have 19 working bulbs and 4 bad ones. This means that the probability that the second bulb works is
`(19)/(23)`.

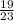Now, we can find our final probability:

`(5)/(6) \cdot (19)/(23) = \boxed{(95)/(138)}`