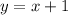Question

What is the equation of the line that passes through (1, 2) and (8,9) in slope-intercept form?

Answer 1

The equation of line that passes through (1, 2) and (8,9) in slope-intercept form is:
`y = x+1`

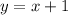
Explanation:

The slope-intercept form of line is given by the formula:

`y = mx+b`

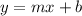
Here m is the slope and b is the y intercept

Given

`(x_1,y_1) = (1,2)\\(x_2,y_2) = (8,9)`

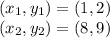
First of all, the slope has to be found

`m = (y_2-y_1)/(x_2-x_1)\\m = (9-2)/(8-1)\\m = 1`

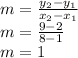
Putting m=1 in the equation

`y = x+b`

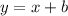
Putting the point (1,2) in the equation to find the value of b

`2 = 1+b\\b = 2-1\\b = 1`

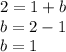
The equation is:

`y = x+1`

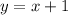
Hence,

The equation of line that passes through (1, 2) and (8,9) in slope-intercept form is:
`y = x+1`