Question

If the angle between each blade of the wind turbine is the same, and each blade has a length of 20 meters, find the distance between the tips of two blades. Round the answer to the nearest hundredth, if necessary. A. 20 meters B. 28.28 meters C. 34.64 meters D. 40.01 meters

Answer 1

A typical windmill has three blades. We can envision these blades in a circle, which a circle = 360 degrees. We want to divide up the angles of the blades so they are even or makes up 360 degrees. We have three blades so we have 3 angles to divide by 360 degrees. So, 360 / 3 = 120 degrees. Now that we know the angle of the blades, we can use the Law of Cos to solve the distance between the blade tip.

Law of Cos

`c^2 = a^2 + b^2 - 2(a)(b)(\cos A)`

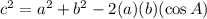
We know

a = 20

b = 20

A = Angle = 120

We need to solve for c

`c^2 = a^2 + b^2 - 2(a)(b)(\cos A)`

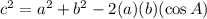
Take the square root of each side of the =

`√(c^2) = √(a^2 + b^2 - 2(a)(b)(\cos A))`

`c = √(a^2 + b^2 - 2(a)(b)(\cos A))`

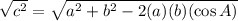
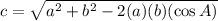
Input the values we know into the formula and solve for c:

`c = √(a^2 + b^2 - 2(a)(b)(\cos A))`

`c = √(20^2 + 20^2 - 2(20)(20)(\cos 120))`

`c = √(400 + 400 - 2(20)(20)(\cos 120))`

`c = √(800 - 2(20)(20)(\cos 120))`

`c = √(800 - 2(400)(\cos 120))`

`c = √(800 - 800(\cos 120))`

`c = √(800 - (-400))`

`c = √(1200)`

`c = 20√(3)`

`c = 34.641016`

`c = 34.64`

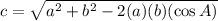
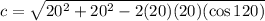
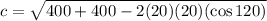
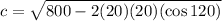
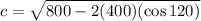
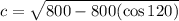
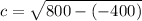
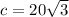
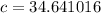
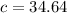
We now have our answer, which is 34.64 and that is C.