Here we need to find fog and gof, and they must be equal to x .
Let's check out fog
fog = f(g(x))
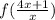
Substituting the value of g(x) in f(x) for x, we will get

Domain
Here the input function is g(x), and the denominator should not be 0. So x should not be zero. Therefore, domain is
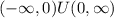
Now let's check gof
gof = g(f(x))
Here we need to insert f(x) in g(x) for x, and on doing that , we will get
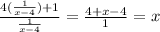
Domain
Here the input function is f(x), and denominator should not be zero.
SO domain is

Since fog = gof =x, so the given function are inverses of each other .