A sequence is arithmetic if the subtraction between any pair of consecutive terms is constant.
A sequence is arithmetic if the ratio between any pair of consecutive terms is constant.
Let's pick consecutive couples and check their difference and ratio:
First couple: first and second term
Difference:
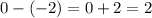
Ratio:
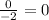
Second couple second and third terms:
Difference:

Ratio:
![(2)/(0) = \text{undefined}]()
So, we can see that the difference remained constant (is always 2), while the ratio isn't even defined. So, this is an arithmetic sequence.
As a corollary, you can see that a geometric sequence can never contain 0. Otherwise, when checking consective ratios, that 0 will eventually be a denominator and break the procedure.