Yes: the function f(n) associates n with the n-th term of the sequence, so f(1) represents the first entry. Moreover, you can verify that the common difference is 7 by considering any pair of adjacent terms, and subtract the latter from the former. For example, with the first two terms, you have
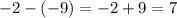
The same goes with the second and third:
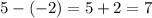
and so on.
A side note: by saying that the answer is correct, I'm assuming that the functions starts form one, i.e., given the sequence
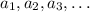 , the function is
, the function is
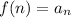 .
.
Nevertheless, some people (me including, actually) use to start the index at zero, so the sequence would become
 . With this notation, f(1) would actually be the second term of the sequence, and the correct answer would be A.
. With this notation, f(1) would actually be the second term of the sequence, and the correct answer would be A.
So, without saying precisely which notation you're following, the answer is a bit ambiguous, but since the
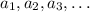 is the most common, I assumed that you were right.
is the most common, I assumed that you were right.