Answer : The two values of 'x' are, 1.192 and -4.192
Step-by-step explanation :
The given expression is,
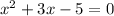
To solve this problem we are using quadratic formula.
The general quadratic equation is,
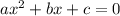
Formula used :

Now we a have to solve the above equation and we get the value of 'x'.
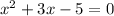
a = 1, b = 3, c = -5

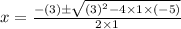
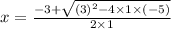
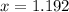
and,
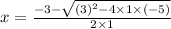
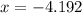
Therefore, the values of 'x' are 1.192 and -4.192