Question

Which of the following is true for the relation f(x) = 2x2 + 1? Only the inverse is a function. Only the equation is a function. Both the equation and its inverse are functions. Neither the equation nor its inverse is a function.

Answer 1

Both the equation listed above and the inverse are functions.

We know that the equation above is a function because firstly, it is a quadratic, which is a type of function. We also know it is a function because there is only 1 output for all of the inputs we can use, or to put it more simply, no matter what x we put in, only one y value comes out.

To find if the inverse is a function, we first have to find the inverse. You can find the inverse to any function by switching the x and f(x) values. After that, solve for the new f(x) value. The result will be the inverse function. The step-by-step process for this one is done below for you.

f(x) = 2x^2 + 1 ----> Switch the x and f(x)

x = 2f(x)^2 + 1 ----> Subtract 8 from both sides

x - 1 = 2f(x)^2 ----> Divide both sides by 2

`(x - 1)/(2)` = f(x)^2 ----> Take the square root of both sides

f(x) =
`\sqrt{(x - 1)/(2)}`

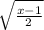
And this is also a function because we only get one output for every input. Therefore, both are functions.