Question

The surface area of two similar solids are 340 yd^2 and 1,158 yd^2. The volume of the larger solid is 1,712 yd^3 what is the volume of the smaller solid

Answer 1

The first thing we must do for this case is find the scale factor.

We have then:

`k^2=(1158)/(340)`

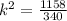
Rewriting we have:

`k^2=3.4`

`k=1.8`

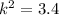
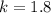
Then, we look for the value of the smallest solid volume.

For this, we have the following relationship.

`V1=k^3V2`

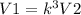
Where,

V1: volume of the largest solid

V2: volume of the smallest solid

k: scale factor

Clearing V2 we have:

`V2 = (V1)/(k^3)`

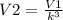
Substituting values we have:

`V2 = (1712)/(1.8^3)`

`V2=293.6`

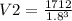
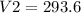
Answer:

the volume of the smaller solid is 293.6 yd^3