Answer: option B
h=-16
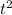 +52t+16
+52t+16
where h is the height of the jet in feet and t is the time in seconds since it is launched.
We need to find the time taken to reach the maximum height.
Highest point is the vertex of the given equation.
To find the x coordinate of vertex we use a formula
t =
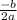
From the given equation
h=-16
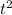 +52t+16
+52t+16
a= -16 , b= 52, c= 16
Plug in the values in the formula
t =
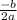
t =
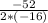
t= 1.625 seconds
Approximately t= 1.6 seconds