The subspace has dimension 3.
Intuitively, you can think that you're removing one degree of freedom from
 . In fact, this space is generated by the following span:
. In fact, this space is generated by the following span:
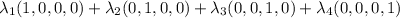
Since the first and third coordinate must be the same, we have
 . So, the span becomes
. So, the span becomes
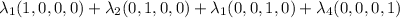
which is the same as
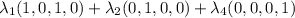
And so you can see that the space is generated by three vectors.