Question

The number of lightning strikes in a year at the top of a particular mountain has a poisson distribution with a mean of 3.8. find the probability that in a randomly selected year, the number of lightning strikes is 0.

Answer 1

Let X be the number of lightning strikes in a year at the top of particular mountain.

X follows Poisson distribution with mean μ = 3.8

We have to find here the probability that in randomly selected year the number of lightning strikes is 0

The Poisson probability is given by,

P(X=k) =
`(e^(-mean) mean^(x))/(x!)`

Here we have X=0, mean =3.8

Hence probability that X=0 is given by

P(X=0) =
`(e^(-3.8) 3.8^(0))/(0!)`

P(X=0) =
`(0.02237 * 1)/(1)`

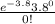
P(X=0) = 0.0224

The probability that in a randomly selected year, the number of lightning strikes is 0 is 0.0224