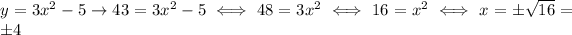Question

Find the domain and range of the function f(x) = 3x^2 - 5.Also find f(-3) and the numbers which are associated with the number 43 in the range.

Answer 1

Domain:

This function is a polynomial, i.e. a sum of powers of a variables, each with its coefficient. Polynomials are defined for every possible value of the variable, so the domain is the whole real number set:
`D = \mathbb{R}`

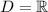
Range:

A polynomial of degree 2 represents a parabola. Since the leading coefficients, i.e. the coefficient of the term with highest degree, is positive (in this case, it's 3), the parabola is concave up. It means that it has a minimum, and it's unbounded from above. So, the range is something like
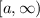`[a,\infty)`. To find the minimum, let's start with the "standard" parabola
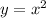`y=x^2`, and transform it to the one of this exercise.
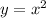`y=x^2` has minimum 0, and thus its range is
`[0,\infty)`. When you multiply it times three, its shape narrows, but the range wont change:
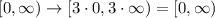`[0,\infty) \to [3\cdot 0,3\cdot \infty) = [0,\infty)`. Finally, when you subtract 5, you shift everythin down 5 units. This transformation affects the range, since you have
`[0,\infty) \to [0-5,\infty-5) = [-5,\infty)`

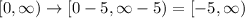
Image of -3:

To compute
`f(-3)`, simply plug
`x=-3` in the formula:

`f(-3) = 3(-3)^2-5 = 3\cdot 9 - 5 = 27-5 = 22`

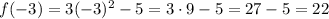
Numbers associated with 43:

We want to see which x value we must choose to get a y value of 43. So, the equation is

`y = 3x^2-5 \to 43 = 3x^2-5 \iff 48 = 3x^2 \iff 16 = x^2 \iff x = \pm√(16) = \pm4`