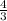Question

F (x) = 3x – 1 and f –1is the inverse of f, what is the value of f –1 (3)?

Answer 1

The value of the inverse at f-1(3) is
`(4)/(3)`.

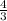To find this, we first need to find the inverse function. We can do so by switching the f(x) and x value. Then we need to solve for the new f(x). The result will be the inverse function. The work for this function is below.

f(x) = 3x - 1 ----> Switch the x and f(x)

x = 3f(x) - 1 ----> Add 1 to both sides

x + 1 = 3f(x) ----> Divide both sides by 3.

f(x) =
`(x + 1)/(3)`

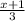
Now that we have the inverse function, we can evaluate it at x = 3

f(x) =
`(x + 1)/(3)`

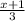
f(3) =
`(3 + 1)/(3)`

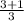
f(3) =
`(4)/(3)`