Solution: We are given:
x bar=34.8
s = 7.1
n=19
The 99% confidence interval for the population mean is given below:
xbar +-
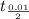
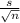
34.8 +- 2.878 (
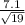 )
)
34.8 +- 4.69
[34.8-4.69,34.8+4.69]
[30.11, 39.49]
Therefore the 99% confidence interval for the population mean is:
30.11≤μ≤39.49
The margin of error is 4.69
There is 99% chance that the confidence interval 30.11≤μ≤39.49 contains the true population mean.