Question

a die is rolled 6 times. let x denote the number of 2s that appear on the die. show that x is a binomial

Answer 1

A die has 6 sides

The probability of getting a 2 in a single throw is
`(1)/(2)`

The probability of not getting a 2 in a single throw is
`(5)/(6)`

The probability of getting one 2 in any of the 6 tosses is

i.e X=1 is given by ₆C₁

multiplied by the probability of getting one 2 in a toss which is 1/6 and the probability of not getting a 2 in one toss which is

`(5)/(6) .(5)/(6) .(5)/(6) .(5)/(6) .(5)/(6)`

so this would combine to ₆C₁ .
`[(1)/(6)]^(1) .[(5)/(6)]^(5)`

Now similarly for X=2

That is the probability of getting two heads in 6 times is

P(X)= ₆C₂ .
`[(1)/(6)]^(2) .[(5)/(6)]^(4)`

(there are two chances of getting 1/6 and 4 chances of getting 5/6)

Similarly for X=3

P(X)= ₆C₃ .
`[(1)/(6)]^(3) .[(5)/(6)]^(3)`

and so on.

Hence this will sum to

P(X=a)= nCa X
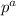`p^(a)` X
`x q^(n-a)`

which is a binomial distribution where

N is the number of tosses

a is the number of desired results or successes

P is the probability of success

q is the probability of failures

Hence this situation follows binomial distribution