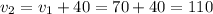Question

two cars start from two towns 500 miles apart travel towards each other.they pass each other after 5 hours.find the speed of each car if the difference between their speeds is 40 miles per hour

Answer 1

Let's say that the two cars travel from city A to city B, and we know that AB = 500m.

Let's also say that we consider city A to sit at x = 0, and city B to sit at x = 500. So, speed is positive for the car going from A to B, and is negative for the car going from B to A.

So, the first car follows this rule:

`s_1 = v_1t`

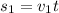
While the second car follows this rule:

`s_2 = 500 - v_2t`

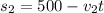
But we know that the difference between their speed is 40, so let's say that

`v2 = v1+40 \implies s_2 = 500 - (v_1+40)t`

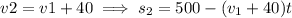
These are the equations that identify the position of the cars after
`t` hours. Since we know that after 5 hours (i.e.
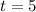`t = 5`) the cars meet, it means that if we plug that value in both equations, we will have the same results. In formulas,

`5v_1 = 500 - 5(v_1+40)`

From here, it's easy to rearrange the equation and solve for the first car's speed:

`5v_1 = 500 - 5v_1+200`

`5v_1 = 700 - 5v_1`

`10v_1 = 700`

`v_1 = 70`

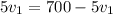
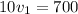
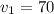
And since the speed of the second car was 40 more than the first one, we have

`v_2 = v_1 + 40 = 70 + 40 = 110`