Question

Divide the sum of -13/5 and 12/7 by the product of -31/7 and -1/2

Answer 1

Let's compute the two factors separately: as for "the sum of -13/5 and 12/7", we have to rewrite the two fractions so that they have the same denominator. Since the least common multiple of 5 and 7 is 35, we will change both fractions so that they have denominator 35:

`(-13)/(5) = (-13)/(5)(7)/(7) = (-91)/(35) \qquad \qquad (12)/(7) = (12)/(7)(5)/(5) = (60)/(35)`

So now we can sum them:

`(-13)/(5)+(12)/(7) = (-91)/(35)+(60)/(35) = (-91+60)/(35) = (-31)/(35)`

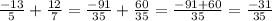
Multiplication is easier, since you just have to multiply numerators and denominators with each others:

`(-31)/(7) (-1)/(2) = (-31 \cdot (-1))/(7\cdot 2) = (31)/(14)`

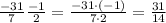
Finally, we must divide the two fractions. Dividing by a fraction is the same this as multiplying by the inverse of that fraction, i.e. we have to switch numerator and denominator:

`(-31)/(35) / (31)/(14) = (-31)/(35) \cdot (14)/(31) = -(2)/(5)`