Question

A rectangular painting has a diagonal measure of 5 inches and an area of 12 square inches. Use the formula for the area of a rectangle and the Pythagorean Theorem to find the length and width of the painting.

Answer 1

The length and width of the rectangular painting are 4 inches and 3 inches, respectively.

Step-by-step explanation:

To find the length and width of the rectangular painting, we will need to apply two mathematical principles:

1. The area of a rectangle is given by the formula A = lw , where A is the area, l is the length, and w is the width.
2. The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (in this case, the diagonal of the rectangle) is equal to the sum of the squares of the other two sides (the length and width of the rectangle). The formula is c^2 = a^2 + b^2, where c is the diagonal, and a and b are the length and width.

Given the information:
1. The diagonal of the painting c = 5 inches
2. The area of the painting A = 12 square inches

Step 1: We can set up the equation for the area of the rectangle:

`\( A = lw \)`

`\( 12 = l \cdot w \)`

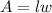
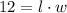
Step 2: Set up the equation for the Pythagorean Theorem:
c^2 = a^2 + b^2
5^2 = l^2 + w^2
25 = l^2 + w^2

Step 3: We have two equations with two unknowns. Let's solve for one variable in terms of the other using the area equation:
\( w = \frac{12}{l} \)

Step 4: Substitute this into the Pythagorean Theorem equation:

`\( 25 = l^2 + \left( (12)/(l) \right)^2 \)`

`\( 25 = l^2 + (144)/(l^2) \)`

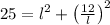
Step 5: Multiply through by l^2 to eliminate the fraction:
25l^2 = l^4 + 144

Step 6: Rearrange the equation to form a quadratic equation:
l^4 - 25l^2 + 144 = 0

Step 7: This resembles a quadratic in form of l^2. Let's use a substitution u = l^2 to make it look like a standard quadratic equation:
u^2 - 25u + 144 = 0

Step 8: Factor the quadratic equation:
(u - 9)(u - 16) = 0

Step 9: Solve for the roots of the equation:
u - 9 = 0 or u - 16 = 0
u = 9 or u = 16

Step 10: Remember that \( u \) was a substitution for \( l^2 \), which means:

`\( l^2 = 9 \) or \( l^2 = 16 \)`

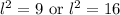
l = 3 or l = 4

Since a rectangle has two different sides, we take both solutions as possible lengths and widths, given that \( l \cdot w = 12 \).

We find:
- If l = 3 , then
`\( w = (12)/(3) = 4 \)`.
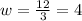- If l = 4 , then
`\( w = (12)/(4) = 3 \)`.

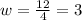Either way, the two sides of the rectangle are 3 inches and 4 inches. Thus, the length and width of the rectangular painting are 4 inches and 3 inches, respectively. These dimensions satisfy both the given area and the diagonal's length according to Pythagorean Theorem.

Answer 2

We have 2 different equations with which we need to work to find the answer to this. First off, the area formula is A = L * W. Our area is 12, so 12 = L * W. Then we have the Pythagorean's theorem we have to worry about, which says that
`5^2=l^2+w^2`. We are going to solve the area equation for L to get
`l=(12)/(w)`. What we are going to do now is sub that into the other formula in place of L to get
`5^2=((12)/(w))^2+w^2` and
`25=(144)/(w^2)+w^2`. In order to solve for w, we need to multiply all those terms by w^2 to get rid of the denominator. That leaves us with this then:
`25w^2=144+w^4`. We need to factor that now to solve for w. We will bring everything over to the one side of the equation and set it equal to 0.
`w^4-25w^2+144=0`. We are going to use a u substitution here to make the factoring easier. We are going to let
`u=w^2` so
`u^2=w^4`. Now we will factor
`u^2-25u+144=0`. When we factor that we get (u - 16)(u - 9). By the Zero Product Property, either u - 16 = 0 or u - 9 = 0. u = 16 and u = 9. But remember that u = w^2, so what we really have, after we make the replacement, is
`w^2=16` so w = 4, and
`w^2=9` and w = 3. Now it just so happens that if the length is 4 and the width is 3, the product of those is 12 (the area), and if you remember, in a right triangle with a hypotenuse of 5, the side lengths will be 3 and 4. So your dimensions of the rectangle are that the length is 4 and the width is 3. There you go!