Answer:
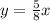
 , when
, when
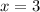 .
.
Explanation:
We have been given that y varies directly with x, and
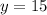 when
when
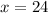 .
.
We know that two direct proportional quantities are in form
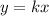 , where k is constant of proportionality.
, where k is constant of proportionality.
Let us find constant of proportionality by substituting
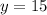 and
and
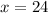 in above equation.
in above equation.
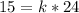
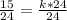
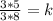
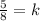
Therefore, our required equation would be
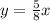 .
.
Let us substitute
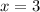 in the equation.
in the equation.


Therefore, the value of y is
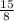 .
.