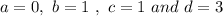Question

Please help!! If the quantity 4 times x times y cubed plus 8 times x squared times y to the fifth power all over 2 times x times y squared is completely simplified to 2xayb + 4xcyd, where a, b, c, and d represent integer exponents, what is the value of a? _______

Answer 1

The value of a is: 0

Explanation:

We are given a expression by:

Quantity 4 times x times y cubed plus 8 times x squared times y to the fifth power all over 2 times x times y squared.

which is mathematically written as:

`=(4xy^3+8x^2y^5)/(2xy^2)`

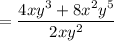
Now, this expression could also be written as:

`=(4xy^3)/(2xy^2)+(8x^2y^5)/(2xy^2)`

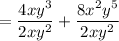
Since,

`(a+b)/(c)=(a)/(c)+(b)/(c)` )

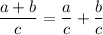Now, on further simplifying we have:

`=2x^(1-1)y^(3-2)+4x^(2-1)y^(5-2)`

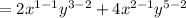
since,

`(x^m)/(x^n)=x^(m-n)`

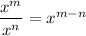
Hence, we have :

`=2x^0y^1+4x^1y^3`

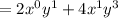
Hence, on comparing it with:

`2x^ay^b+4x^cy^d`

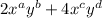
we have:

`a=0,\ b=1\ ,\ c=1\ and\ d=3`

Answer 2

You want the exponent of x in the first term of ...

`(4xy^3+8x^2y^2)/(2xy^2)=(4)/(2)x^((1-1))y^((3-2))+(8)/(2)x^((2-1))y^((2-2))\\\\=2x^0y^1+4x^1y^0`

The exponent a is 0.