Question

Given the trinomial, what is the value of the coefficient 'B' in the factored form? (2 points) 2x2 − 12xy − 32y2 = 2(x − 8y)(x + By)

Answer 1

2x^2 − 12xy − 32y^2

= 2(x^2 - 6xy - 16y^2)

= 2(x - 8y)(x + 2y)

Answer

B = 2

Answer 2

The value of B is 2.

Explanation:

The given trinomial is

`2x^2-12xy-32y^2`

Taking out the GCF.

`2(x^2-6xy-16y^2)`

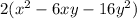
The middle term can be written as -8xy+2xy.

`2(x^2-8xy+2xy-16y^2)`

`2(x(x-8y)+2y(x-8y))`

`2(x-8y)(x+2y)`

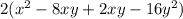
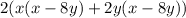
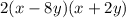
The factored form of the given trinomial is 2(x-8y)(x+2y). The given factored form of the trinomial is 2(x − 8y)(x + By). Equate both factored form.

`2(x-8y)(x+2y)=2(x-8y)(x+By)`

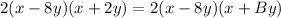
On comparing both the sides we get

`B=2`

Therefore the value of B is 2.