Question

A cone’s height is reduced to 3/8 of its original length, and its radius is tripled. How has the volume of the cone changed?

Answer 1

Cone Volume = PI * radius^2 * height / 3

So if radius = 1 and height = 1 then volume = 1.0472

When radius = 3 and height = .375 then volume = 3.5343

Volume increases by 3.5343 / 1.0472 = 3 and 3/8

Answer 2

The new volume will be
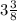`3(3)/(8)` of its original volume.

Explanation:

If the height of a cone is
`h` and the radius is
`r`, then its volume is:
`(1)/(3)\pi r^2 h`

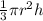
Now, the height is reduced to
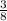`(3)/(8)` of its original length, and its radius is tripled.

That means, the new height
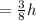`= (3)/(8)h` and the new radius
`= 3r`

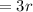
So, the new volume will be:
`(1)/(3)\pi (3r)^2((3)/(8)h) =(1)/(3)\pi (9r^2)((3)/(8)h)=(27)/(24)\pi r^2h=(9)/(8)\pi r^2h`

Now,

`((9)/(8)\pi r^2h)/((1)/(3)\pi r^2 h) \\ \\ =((9)/(8))/((1)/(3))=(9)/(8)* (3)/(1)=(27)/(8)=3(3)/(8)`

Thus, the new volume will be
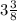`3(3)/(8)` of its original volume.