Question

How do we solve this ?

Answer 1

I visited Indonesia in 1991 but all I can say now is "saya mau beli mango."

It's probably more correct to call the graph (one dimensional) position versus time rather than distance versus time.

(i) The speed will be the slope of the position versus time graph, so in the first ten seconds that's

`\frac{60 \textrm{ meters} - 20 \textrm{ meters}}{10 \textrm{ seconds} - 0 \textrm{ seconds}} =4 \textrm{ meters per second}`

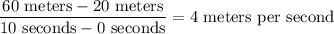
(ii) The speed is zero when the slope is zero, or flat, horizontal. That's from t=10 seconds to t=20 seconds.

(iii) The last 10 seconds we went from a position of 60 to a position of zero; i.e. we went backwards. That's a speed or slope of

`\frac{0 \textrm{ meters} - 60 \textrm{ meters}}{25 \textrm{ seconds} - 20 \textrm{ seconds}} = -12 \textrm{ meters per second}`

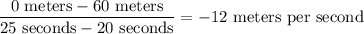
Technically the speed is the absolute value of this velocity, 12 meters per second.

(iv) The average speed is the total change in position over the total time.

`\frac{0 \textrm{ meters} - 20 \textrm{ meters}}{25 \textrm{ seconds} - 0 \textrm{ seconds}} = -0.8 \textrm{ meters per second}`

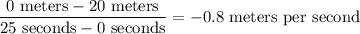
Again technically the speed is the absolute value of that, 0.8 meters per second.