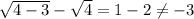Question

Solve √(y-3)-√y = -3

Answer 1

This equation has no solutions

Move the square root of y to the right hand sides:

`√(y-3) = √(y)-3`

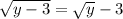
To eliminate the roots, let's square both sides. But there is a crucial observation in this passage: you are allowed to deduce
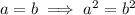`a=b \implies a^2=b^2` only if both
`a` and
`b` are positive. Otherwise, you risk contraddictions like
`2 = -2 \implies 4 = 4`.

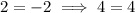Since the left hand side is always positive when defined (it's a square root), we need to ask
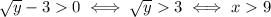`√(y)-3 > 0 \iff √(y) > 3 \iff x>9`. So, we're only accept answers if they're greater than nine.

Now we can square both sides:

`y-3 = y- 6√(y) + 9`

Simplify y's and bring 9 to left hand side:

`-12 = -6√(y)`

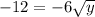
Divide both sides by -6:

`2 = √(y) \implies y = 4`

So, the solution is not acceptable. In fact, it would lead to

`√(4-3) - √(4) = 1-2 \\eq -3`