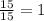Question

A number is chosen at random from the set of numbers (21,22,23,.......34,35) what is the probability that it is

A multiple of 4, a prime number, the number 18, a whole number

Answer 1

In cases like this, the probability of a certain event is given by the ratio between the positive outcomes, and all positive outcomes. There are
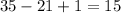`35-21+1 = 15` numbers in your set. The positive outcomes depend on the request:

There are three multples of four, namely 24,28 and 32. So, the probability of choosing one of them is
`(3)/(15)=(1)/(5)`

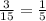
There are three prime numbers, namely 23,29 and 31. So, the probability of choosing one of them is
`(3)/(15)=(1)/(5)`

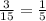
The number 18 doesn't belong to the set, so you can't possibly choose it. In other words, there are zero positive outcomes, so the ratio becomes
`(0)/(15) = 0`

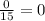
All of the numbers in the set are whole number, so you are certain that you will chose a whole number. In other words, all 15 possible outcomes are positive outcomes, so the ratio becomes
`(15)/(15) = 1`