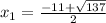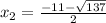This is a quadratic equation, i.e. an equation involving a polynomial of degree 2. To solve them, you must rearrange them first, so that all terms are on the same side, so we get
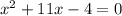
i.e. now we're looking for the roots of the polynomial. To find them, we can use the following formula:
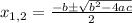
where
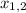 is a compact way to indicate both solutions
is a compact way to indicate both solutions
 and
and
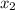 , while
, while
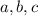 are the coefficients of the quadratic equation, i.e. we consider the polynomial
are the coefficients of the quadratic equation, i.e. we consider the polynomial
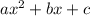 .
.
So, in your case, we have
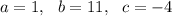
Plug those values into the formula to get
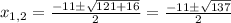
So, the two solutions are