It would help to have the question. But I'll guess
![\sqrt[4]{x^(\frac 3 5)}{√(x^2)} = ((x^(\frac 3 5))^(\frac 1 4)) }{ x} = x^{\frac 3{20}} x = x \sqrt[20]{x^3}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/v0kx7zn5fy9pz17rkkyzt1adqb35ik0uax.png)
2nd choice.
I forgot the explanation because I was so glad to have puzzled out the question.
The fourth root is the same as the 1/4 th power.
If we know x is positive
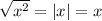
![\sqrt[4]{x^(\frac 3 5)}{√(x^2)}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/lxx8a17mzigef158dxsdvhd01f1csys1a0.png)
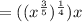
We multiply the powers:
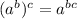
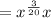
The one-twentieth power is the twentieth root. We bring the additional factor of x to the front.
![= x \sqrt[20]{x^3}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/v3hm1czoucizalddgwb78xkmnamyzasutv.png)