Question

A hollow sphere of radius 0.25 m is rotating at 13 rad/s about an axis that passes through its center. the mass of the sphere is 3.8 kg. assuming a constant net torque is applied to the sphere, how much work is required to bring the sphere to a stop?

Answer 1

The work required to bring the sphere to stop is equal to the kinetic energy possessed by the sphere.

Kinetic energy of a rotating body is given by,

K.E =
`(1)/(2)Iw^(2)`

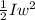
Here, I= Moment of inertia of hollow sphere,

Since, the hollow sphere is rotating about the axis passing through its center, I =
`(2)/(3)MR^(2)`

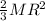
M= Mass of the sphere= 3.8 kg,

R= Radius of gyration= Radius of the sphere= 0.25 m

w= Angular speed of the sphere = 13 rad/s

Substituting the values,

Kinetic energy =
`(1)/(2) *(2)/(3) (3.8)(0.25)^(2)(13.0)^(2)`

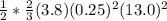
= 13.4 J

∴ Work required to bring the sphere to stop is 13.4 J.