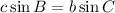Question

Pleaseee Helpp!!!

Given: In △ABC, AD ⊥ BC Prove: What is the missing statement in Step 6? a. b = c b. h/b=h/c C. csin(B) = bsin(C) D. bsin(B) = csin(C)

Answer 1

In step 6 we substitute the value we just found for h in step 5 into the equation in step 3. That's also an equation for h, so we're just setting the other sides equal:

`c \sin B = b \sin C`

Third choice.

Answer 2

Given: In ΔABC ,
`AD \perp BC`

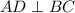
To prove that:
`(\sin B)/(b) =(\sin C)/(c)`

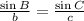
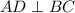`AD \perp BC` [Given]

In ΔADB

The sine angle is defined in the context of a right triangle is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle.

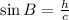`\sin B =(h)/(c)` [By definition of sine] .....[1]

Multiplication Property of equality states that you multiply both sides of an equation by the same number.

Multiply by c to both sides of an equation [1] we get;

`c \cdot \sin B =c \cdot(h)/(c)`

Simplify:

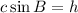`c \sin B = h` ......[2]

Now, In ΔACD

Using definition of sine:

`\sin C =(h)/(b)`

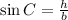
Multiply both sides of an equation by b;

`b \cdot \sin C = b \cdot (h)/(b)` [Multiplication Property of equality]

Simplify:

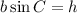`b \sin C = h` ......[3]

Substitute [3] in [2];

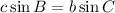`c \sin B = b \sin C` ......[4]

Division property of equality states that if you divide both sides of an equation by the same nonzero number the sides remains equal.

[4] ⇒
`(\sin B)/(b) =(\sin C)/(c)`

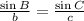
Therefore, the missing statement in step 6 is;
`c \sin B = b \sin C`