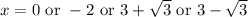Question

What are the roots of the equation x^4- 4x^3=6x^2- 12x. Using a graphing calculator and system of roots.

Answer 1

I don't have a graphing calculator and I don't know what the system of roots is.

But I can solve this anyway.

x^4 - 4x^3 - 6x^2 + 12 x = 0

x(x^3 - 4x^2 - 6x + 12) = 0

So x = 0 is a root and we have a cubic equation to solve.

In school the best way to solve cubic equations is to just try some small numbers; teachers seldom venture beyond 1, -1, 2 or -2 as roots. I guess a graphing calculator saves us the search.

Here we see x=-2 is a root; (-2)^3 - 4(-2)^2 - 6(-2) + 12 = -8 - 16 + 12 + 12 = 0.

So, continuing our factoring, x+2 is a factor, and we divide to get the other factor

x^2 - 6x + 6

x+2 | x^3 - 4x^2 - 6x + 12

x^3 + 2x^2

-6x^2 - 6x

- 6x^2 - 12 x

6x + 12

So fully factored we have

0 = x(x+2)( x^2 - 6x +6 )

There's a little shortcut I call the Shakespeare Quadratic Formula (2b or -2b) which works when the linear term is even:

`x^2 - 2bx + c \textrm{ has zeros } x =b \pm √(b^2-c)`

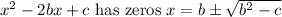
Here that means we have two additional roots,

`x = 3 \pm √(3^2-6) = 3 \pm √(3)`

Full set of roots:

`x = 0 \textrm{ or } -2 \textrm{ or } 3 + √(3) \textrm{ or } 3 - √(3)`