Question

UMM HELP???Sully manages a cafe that typically sells 240 cups of coffee per day for $2 each. Sully knows that for each $0.25 increase in the price of coffee, 20 fewer cups of coffee will be sold. Let x represent the number of $0.25 price increases and f(x) represent the total revenue earned from coffee sales.

Answer 1

We need to write f(x), the revenue as a function of the price increase. When x=0 the coffee price is $2, unit sales 240, and revenue 2(240)=$480. When x=1 the coffee price is $2.25, unit sales 220 and revenue 2.25(220) =$495.

In general the coffee price is 2 + 0.25 x and the unit sales are 240 - 20 x. The revenue is the product:

`f(x) = (2 + 0.25 x ) (240 - 20 x) = 20(2+0.25x )(12 - x) = -5(x+8)(x-12) = -5(x^2 - 4 x - 96)`

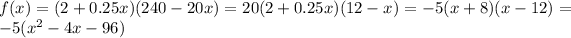
That's the function for the first blank; other variations are possible.

The second blank must be "maximum;" -- why else would Sully do this?

Not sure if we're in calculus or algebra here; for calculus we'd maximize by setting the derivative to zero and solving for x; in algebra we'd complete the square. Let's complete the square.

`f(x) = -5(x^2 - 4 x - 96) = -5( x^2 - 4x +4 -96 -4) = -5( (x-2)^2-100)`

At x=2 the squared term is zero so we're at our maximum of -5(-100)=$500

That's revenue ... will be $500 after 2 quarter price increases.