Question

Find the area of a segment formed by a chord 8" long in a circle with radius of 8".

Answer must be in A=(n*pi-n(sqrt(n))) sq. in. format.

Answer 1

This is a circle with the radii forming a piece of pizza that is the sector, and the chord goes from the endpoint of one radii to the endpoint of the other radii which is the base of a triangle that uses the radii as sides. So we have to find the area of the sector and then subtract from it the area of the triangle, leaving the area between the segment and the outside of the circle. For the area of the sector...we need the central angle. if we look to the triangle that is formed with the chord and the 2 radii, we see that all the sides of that triangle measure 8". If all the sides are the same, by the converse of the Isosceles Triangle Theorem, then all the angles are the same measure as well. This means that this is an equiangular triangle and all the angles measure 60 degrees (by the Triangle Angl-sum Theorem all the angles of a triangle add up to equal 180). So the central angle is 60. Our formula for the sector then is this:
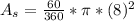`A_(s)=(60)/(360)*\pi *(8)^2` which simplifies to
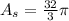`A_(s)=(32)/(3)\pi`. Now we will go to the triangle formed by the chord and the 2 radii. The formula for a triangle is
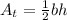`A_(t)=(1)/(2)bh`. We know the base is 8. That was given to us as the measure of the chord. The height, however, is a different story. If we extract this triangle and drop an altitude from the vertex angle to the base, that is the height we are looking for the h in our formula. If all the angles of the whole triangle are 60 degrees, when we drop the altitude, we are cutting that vertex angle exactly in half. So half of our whole triangle is a 30-60-90 triangle, with the base angle as 60 degrees. The side across from the 60 degree angle in the Pythagorean triple is the square root of 3. So filling in our formula for the area we have
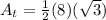`A_(t)=(1)/(2)(8)(√(3))` which simplifies down to
`A_(t)=4√(3)`. Now go back to the beginning where we said that the area of that little bit of the circle between the chord and the outside of the circle was found by subtracting the area of the triangle from the area of the sector. Leaving it in the form in which you need it looks like this:
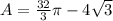`A=(32)/(3)\pi -4√(3)`. There you go!