Question

Simplify the radical expression.

Answer 1

To simplify this fraction, multiply the entire fraction by the conjugate of the denominator. The conjugate of a square root and a number being added to it would be the number subtracted from the square root. In other words, the conjugate of
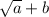`√(a) + b` would be
`√(a) - b`.

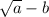Applying that information to our fraction shown here, the conjugate of the denominator would be
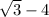`√(3) - 4`. We will multiply both the numerator and denominator of our original fraction by this expression to obtain our answer, as shown below.

`\Big((1)/(√(3) + 4)\Big)\Big((√(3) - 4)/(√(3) - 4)\Big)`

`(√(3) - 4)/(3 - 16)`

`(4 - √(3))/(13)`

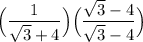
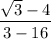
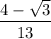
Our answer is
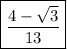`\boxed{(4 - √(3))/(13)}`.