For this case we have the following expressions:
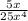
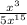
We can rewrite both expressions using properties of powers.
For power properties we have:
"In a division, if we have the same base, we subtract the exponents"
Rewriting both expressions we have:
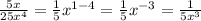
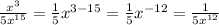
Answer:
True.
Rational expressions are not equivalent.