Let X be the score of the test. X follows normal distribution with mean μ = 70 and standard deviation σ =12
The percentage of scores that will fall below 50 is
P(X < 50) =
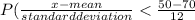
= P(z < -1.67)
Using standard normal probability table to find probability below -1.67
P(X < 50) = P(Z < -1.67) = 0.0475
The probability that scores will fall below 50 is 0.0475
Converting probability into percentage
0.0475 * 100 = 4.75
The percentage of score will fall below 50 is 4.75%