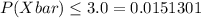Question

Major league baseball salaries averaged $3.26 million with a standard deviation of $1.2 million in a recent year. suppose a sample of 100 major league players was taken. find the approximate probability that the mean salary of the 100 players was no more than $3.0 million.

Answer 1

The approximate probability that the mean salary of 100 players is no more than $3.0 million is 0.0151.

We follow these steps to arrive at the answer:

We have

Population Mean (μ) = $3.2 million

Sample Mean (X bar) = $3.0 million

Population Standard Deviation (σ) = $1.2 million

Sample Size (n) = 100

We use the following formula to find the Z score with the data listed above:

`Z = (Xbar - \mu )/((\sigma )/(√(n)))`

`Z = (3.0 - 3.26)/((1.2 )/(√(100)))`

`Z = (-0.26)/(0.12)`

`Z = -2.1666667`

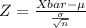
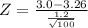
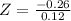
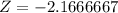
We can refer to the Z tables or use an online calculator to find an area under the normal curve.

Since we need to find the probability that mean salary is no more than $3.0 million, we need to find the area to the left of the calculated Z score.

`P(X bar) \leq 3.0 = 0.0151301`