Question

Helium is pumped into a spherical balloon at the constant rate of 25 cubic feet/minute. at what rate is the surface area of the balloon increasing at the moment when its radius is 8 feet?

Answer 1

If we let V', A', and r' represent the rates of change of the volume, area, and radius of the sphere, we can differentiate equations for V and A in terms of r, then eliminate r' to get an equation for A' in terms of V'.

`V=(4)/(3)\pi r^(3)\\V^(\prime) =4\pi r^(2)\cdot r^(\prime)\\\\A=4\pi r^(2)\\A^(\prime) =8\pi r\cdot r^(\prime)\\\\A^(\prime)=8\pi r\cdot (V^(\prime))/(4\pi r^(2))=(2)/(r)V^(\prime)`

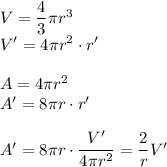
Then, for the given values, the surface area is increasing at the rate ...

... A' = (2/8)·25 ft²/s = 6.25 ft²/s