Since you don't provide the coordinates of the point W, I will help you in a general form anyway. In the Figure below is represented the segment that matches this problem. We have two endpoints U and V. So, by using the midpoint formula we may solve this problem:

Therefore:
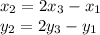
So we know
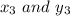 but we also must know
but we also must know

Finally, knowing the points U and W we can find the endpoint V.