The answer is the first option, which is:
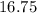 cubic inches.
cubic inches.
The explanation for this answer is shown below.
1. You must apply the formula for calculate the volume of a cylinder and the formula for calculate the volume of a sphere and substitute the values which are given in the problem above, as following:
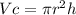
Where
 is the heigth of the cylinder and
is the heigth of the cylinder and
 is the radius.
is the radius.
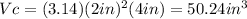
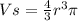
Where
 is the radius of the sphere.
is the radius of the sphere.
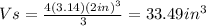
2. Then, you must susbtract both volumes to calculate the difference asked in the problem:
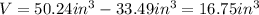
3. Therefore, the answer is the option mentioned above.