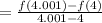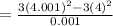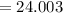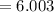Answer:
Since, for a function f(x),
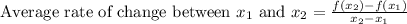
Given function,
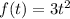
Thus,
(a) the average rate of change of f(t) between t=1 and t=1.001
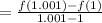
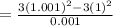
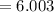
(b) the average rate of change of f(t) between t=2 and t=2.001
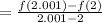

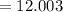
(c) the average rate of change of f(t) between t=3 and t=3.001
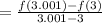
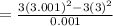
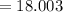
(d) the average rate of change of f(t) between t=4 and t=4.001