Question

A table representing the function f(x)=2(3/2)^x is shown below. What is true of the given function?

Answer 1

The function increases at a constant multiplicative rate. This is because as x increases by 1, f(x) is multiplied by a factor of 1.5.

You see this because if you divide 3/2 you get 1.5 or alternatively you can do 4.5/3 = 1.5 or 6.75/4.5 = 1.5.

Answer 2

Option B.

Explanation:

The given function is
`f(x)=2((2)/(3))^(x)`

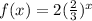
From the given table we can say when we increase x by 1 (from 0 to 1) value of function is
`2((3)/(2))^(0)=2`

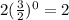
Now we increase x by 1 (from 1 to 2) then value of the function will be

`f(x)=2((3)/(2))^(1)=3`

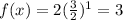
Therefore we see the common ratio of the function value is 3/2 = 1.5

Similarly for the other values of x = 2, 3 we find he value of the function = 4.5, 6.75

Which shows the common ratio as 1.5 for every value of the function.

So we conclude with the increase of x function increases by at a constant multiplicative rate.

Option B is the answer.