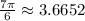Question

Convert 210° from degrees to radians. Use the value of π found on a calculator, and round answers to four decimal places, as needed. (1 point)

a. seven pi divided by twelve

b. seven pi divided by three

c. seven pi divided by five

d. seven pi divided by six

Answer 1

7pi/6

Explanation:

Look at Unit circle 210 degrees

Answer 2

The answer is
`(7\pi)/(6) \approx 3.6652`

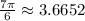
You can easily convert angles by using proportions. The starting point is knowing that
`\pi` radians are 180 degrees.

Now, if we double the angles we will have that
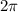`2\pi` radians are 360 degrees. Or, for example, if we half the angles we will have that
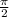`(\pi)/(2)` radians are 90 degrees, and so on.

So, in general, we have the following proportion:

`\pi / 180^\circ = \alpha / \alpha^\circ`

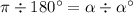
Where
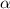`\alpha` and
`\alpha^\circ` are the same angle expressed in radians and degrees, respectively. In this example, we know the angle expressed in degrees, and want to solve the proportion for the angle expressed in radians, so we have

`(\alpha^\circ\pi)/(180^\circ) = \alpha`

Plugging the values, we have

`\alpha = (210\pi)/(180) = (7\pi)/(6)`

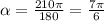
Using a calculator, you can round this value to

`(7\pi)/(6) \approx 3.6652`