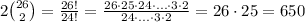Question

an ordinary deck of playing cards, 26 red and 26 black. if a card is dealt to each of 2 players, in how many ways can both cards be red ?

Answer 1

The answer is 325 or 650, depending on how you count consider two cases ti be different.

We can assume that both players are dealt a red card - we're not looking for the probability for this to happen, but rather in how many ways this can happen.

So, we basically want to know how many couples you can extract from a set with 26 elements.

Luckily, there's a powerful tool that deals with this kind of computations: the binomial coefficient. You write and compute it as

`\binom{n}{k} = (n!)/(k!(n-k)!)`

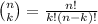
where
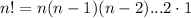`n! = n(n-1)(n-2)...2\cdot 1` is the factorial of
`n`, i.e. the product of all numbers from 1 to
`n`, included.

Now, the question slipped through a little detail, which is nevertheless important for the answer. Imagine that we deal the two player a certain couple of red cards - say that player 1 gets the ace of hearts and player 2 gets the aces of diamonds. Now swap the cards. Does this combination counts as a new one, or do we consider it the same?

If we count the two combinations as one, i.e. we're only interested in the couple of cards dealt, and we don't care about which player got which card, we're good: the answer is exactly

`\binom{26}{2} = (26!)/(2!24!) = (26\cdot 25 \cdot 24 \cdot \ldots \cdot 3\cdot 2)/(2 \cdot 24 \cdot \ldots \cdot 3\cdot 2) (26\cdot 25)/(2) = 13\cdot 25 = 325`

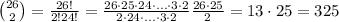
On the other hand, if we consider the two cases as different and want to count them both, we need to multiply all of the 325 possible cases twice, since for any given combination we can swap the cards. So, the answer becomes

`2\binom{26}{2} = (26!)/(24!) = (26\cdot 25 \cdot 24 \cdot \ldots \cdot 3\cdot 2)/(24 \cdot \ldots \cdot 3\cdot 2) = 26\cdot 25 = 650`